Leetcode - Maximum Non Negative Product in a Matrix

October 05, 2020

Problem Statement

You are given a rows x cols matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.

Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (rows - 1, cols - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.

Return the maximum non-negative product modulo 109 + 7. If the maximum product is negative return -1.

Notice that the modulo is performed after getting the maximum product.

Example

Input: grid = [[-1,-2,-3],
               [-2,-3,-3],
               [-3,-3,-2]]
Output: -1 (Not found any non-negative product)

Input: grid = [[1,-2,1],
               [1,-2,1],
               [3,-4,1]]
Output: 8  (1 * 1 * -2 * -4 * 1 = 8)

Input: grid = [[1, 3],
               [0,-4]]
Output: 0 (1 * 0 * -4 = 0).

Input: grid = [[ 1, 4,4,0],
               [-2, 0,0,1],
               [ 1,-1,1,1]]
Output: 2 (1 * -2 * 1 * -1 * 1 * 1 = 2).

Solution-1 (A simple recursive solution)

Please note the restrictions:

You can move either right or bottom.
You can move one step at a time.
You can not stop on finding a negative product. You might get another negative number which can make product positive.
For final maximum non-negative product, you need to take module of 10^9 + 7

In every solution, we will traverse like below:

Matrix Non Negative Product

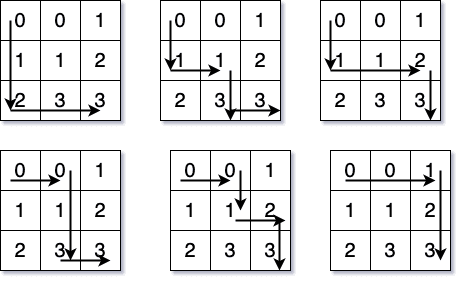
Lets look at the algorithm:

Start from top left corner
For each movement and valid cell location, save that number in a list. We will need this list when we reach to far end and calculate the product.
Move to one row ahead and call same method recursively
Move to one colum ahead and call same method recursively
Check if we reached till far end (Right bottom of matrix) If yes, we need to calculate the product from our list. And remove that element from list.
Finally remove the item from list.

Code

private long prod = -1;
private int modulo = (int)Math.pow(10, 9) + 7;

private long getProd(List<Integer> list) {
  long p = 1;
  for (Integer item : list) {
    p *= item;
  }
  return p;
}

private void find(int[][] grid, int x, int y, List<Integer> list) {
  if (x < grid.length && y < grid[0].length) {
    list.add(grid[x][y]);
  }
  
  if (x == grid.length-1 && y == grid[0].length-1) {
    //find product
    this.prod = Math.max(this.prod, this.getProd(list));
    list.remove(list.size()-1);
    return;
  }
  else if (x >= grid.length || y >= grid[0].length) {
    return;
  }
  
  find(grid, x+1, y, list);
  
  find(grid, x, y+1, list);
  
  list.remove(list.size()-1);
}

public int maxProductPath(int[][] grid) {
  List<Integer> list = new ArrayList<Integer>();
  this.find(grid, 0, 0, list);
  
  return (int)this.prod % this.modulo;
}

You can re-write above find() as below:

private void find(int[][] grid, int x, int y, List<Integer> list) {
  list.add(grid[x][y]);
  
  if (x == grid.length-1 && y == grid[0].length-1) {
    //find product
    this.prod = Math.max(this.prod, this.getProd(list));
    list.remove(list.size()-1);
    return;
  }
  
  if (x+1 < grid.length) {
    find(grid, x+1, y, list);
  }
  
  if (y+1 < grid[0].length) {
    find(grid, x, y+1, list);
  }
  
  list.remove(list.size()-1);
}

Complexity

Its O(n^3), as for every cell, you are traversing the whole matrix (almost)

Another Solution (Another re-write of above solution)

Basically, where we need to calculate the product of the list, we can pass the product as parameter to the function. And, we don’t need to keep the list now.

See

private long prod = -1;
private int modulo = (int)Math.pow(10, 9) + 7;

private void find(int[][] grid, int x, int y, long product) {
  if (x >= grid.length || y >= grid[0].length) {
    return;
  }
  if (x == grid.length-1 && y == grid[0].length-1) {
    this.prod = Math.max(this.prod, product * grid[x][y]);
    return;
  }
  
  find(grid, x+1, y, product * grid[x][y]);
  
  find(grid, x, y+1, product * grid[x][y]);
}
public int maxProductPath(int[][] grid) {
  List<Integer> list = new ArrayList<Integer>();

  long product = 1;
  this.find(grid, 0, 0, product);
  
  return (int)this.prod % this.modulo;
}

Complexity

Its same as above O(n^3)

Optimized Solution - O(n^2)

If you see closely, we are repeating our calculations again and again for some cells. We can save those results in a temporary cache. This solution is called DP (Dynamic Programming).

private long prod = -1;
private int modulo = (int)Math.pow(10, 9) + 7;

private long getProd(List<Integer> list) {
  long p = 1;
  for (Integer item : list) {
    p *= item;
  }
  return p;
}

private void find_dp(int[][] grid, int x, int y, List<Integer> list, int[][] dp) {
  if (dp[x][y] != 0) {
    this.prod = Math.max(this.prod, dp[x][y]);
    return;
  }
  if (x < grid.length && y < grid[0].length) {
    list.add(grid[x][y]);
  }
  
  if (x == grid.length-1 && y == grid[0].length-1) {
    //find product
    this.prod = Math.max(this.prod, this.getProd(list));
    dp[x][y] = (int)this.prod;
    list.remove(list.size()-1);
    return;
  }
  else if (x >= grid.length || y >= grid[0].length) {
    return;
  }
  
  find(grid, x+1, y, list);
  
  find(grid, x, y+1, list);
  
  list.remove(list.size()-1);
}

public int maxProductPath(int[][] grid) {
  List<Integer> list = new ArrayList<Integer>();

  int[][] dp = new int[grid.length][grid[0].length];
  this.find_dp(grid, 0, 0, list, dp);
  
  return (int)this.prod % this.modulo;
}