Counting Sort Algorithm

Counting sort runs on relatively smaller set of input. Counting sort calculates, for every element in array - X, the number of elements which are lesser than - X. It then use this information to put X directly into its position in sorted array.

Selection sort takes two additional array.

• One for result, the sorted array
• other for temporary storage, where size equals to the maximum number on input array.

Its interesting to note that this algorithm is not a comparison sort. You will not see any comparison in code. This algorithm uses elements values to index into array.

Count Sort Algorithm

• First iterate on input array, and calculate each number occurence in the 2nd additional array (lets call it C).
• After the iteration, The array-C’s index will denote the input number, and the value contains how many times the number comes in original array. In the image above, see part-a.
• Run one more iteration on array-c. And, accumulate the sum. See above image, part-b

• Now iterate equal to length of original array (from last index to 0):

  • For the number in original array, use it as index in array-C, which will give you its position in sorted array
  • Put this number in sorted array at position told by array-c
  • Decrement this value from array-c by 1
• At the end, we will get sorted array.

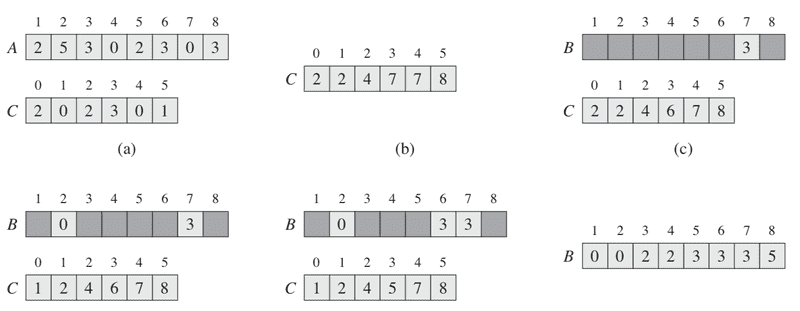
See the code here:

public class CountSort {
    private int[] arr;

    public CountSort(int[] arr) {
        this.arr = arr;
    }

    /**
     * Count sort, max value-k
     * @param k, the max value in array
     */
    public int[] doSort(int k) {
        int[] c = new int[k+1];

        //count number of occurence
        for (int i=0; i<this.arr.length; i++) {
            c[this.arr[i]] ++;
        }

        //accumulate
        for (int i=1; i<c.length; i++) {
            c[i] += c[i-1];
        }
        int[] result = new int[this.arr.length];

        //put the number to its designated place
        for (int i=this.arr.length-1; i>=0; i--) {
            result[c[this.arr[i]]-1] = this.arr[i];
            c[this.arr[i]] --;
        }

        return result;
    }
}

Key Points

• It is not a comparison sort.
• It is a stable sort.
• This uses 2 additional arrays.
• It is used for relatively smaller set of numbers.
• The maximum number in array should be order of size of array. Example: this algorithm is good for sorting age of people.
• Performance is very good. its time complexity is O(n + k) ~= O(n)

Runtime complexity

The algorithm runs on time complexity of O(n + k) ~= O(n) in worst/average case.