Quick Sort Algorithm

This algorithm is very useful for large input. And, is quite efficient one. It has several implementation, and it is proved that for practical cases, it is better than Merge Sort, Heap Sort any many other algorithms. Although, its worst complexity is O(n^2).

This is again an implementation of of Divide and Conquer algorithms. In this algorithm, we first find a pivot element, put it in a position such that every element in left is less than or equal than this. And every element on right side is greater than equal than this number.

So, this pivot element divides the array into two parts. Then, natural recursive algorithm work on individual smaller arrays. Note: It is very important to choose correct pivot element. This algorithm works best when pivot element divides the array into almost equal halves. That is the reason, there are several implementations are available for selecting pivot element.

In a simple implementation, we simply choose the last element as pivot. Some algorithms choose a random pivot element.

Quick Sort Algorithm

• First, we call partition on the array, where lies the main logic of putting the pivot element to correct position.
• Pivot element divides the array into two partitions.
• Now, runs the recursive method on the two partitions.
• Ultimately, partition sorts the sub-array.

See the code here:

public static int partition(int[] arr, int l, int r) {
    int p = r;  //pivot
    
    int sm = l;
    for (int i=l; i<r; i++) {
        if (arr[i] < arr[p]) {
            ArrayUtils.swap(arr, i, sm);
            sm++;
        }
    }
    ArrayUtils.swap(arr, sm, p);
    return sm;
}

public static void qsort(int[] arr, int l, int r) {
    if (l < r) {
        int p = partition(arr, l, r);
        
        qsort(arr, l, p-1);
        qsort(arr, p+1, r);
    }
}

The main logic resides in partition() method. We just kept an index variable: sm which keeps track of all smaller number than our pivot element. And, finally swap our index sm and pivot element index.

Graphical Example

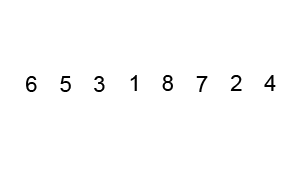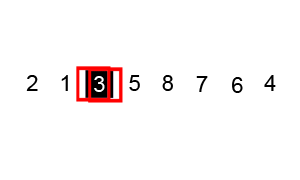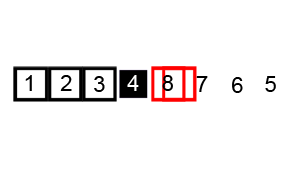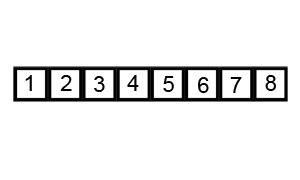
Key Points

• It does not use extra memory.
• Very efficient in sorting large number set.
• Practically best performer than merge sort, if implemented better for selecting pivot element.
• Performance is very good. Average complexity is O(n log n)
• Based on Divice and Conquer technique
• It works well in virtual memory environment

Runtime complexity

The average runtime is O(n log n), but worst case is O(n^2)