Find the maximum sum of any continuous subarray of size K

Introduction

You are given an array of integers with size N, and a number K. Find the maximum sum of continuous subarray of size K.

Example

Input: [1, 2, 6, 2, 4, 1], k=3 
Output: 12
Explanation: Subarray with maximum sum is [6, 2, 4].

Solution (Brute Force)

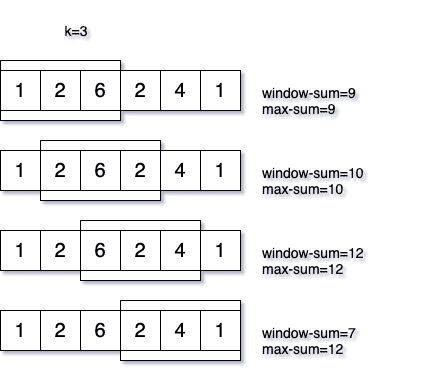
You need to keep sum of the subarray of size=k all the time, and keep on iterating.

Code

public int findMaxSum(int[] arr, int k) {
  int max=0;
  for (int i=0; i<=arr.length-k; i++) {
    int sum_k = 0;
    for (int j=i; j<i+k; j++) {
      sum_k += arr[j];
    }
    max = Math.max(max, sum_k);
  }
  return max;
}

Complexity

There are two loops

1. n-k times != n
2. k times

Total of O(nk)*

Solution (Sliding Window Pattern)

If you observe problem and above solution closely,

• you need to keep continuous array
• size should be K

When you first calculate sum of the first window size of K. You already have the sum of previous window. To get the sum of next window. You need to remove first number of previous window, and add next number. So effectively you are using the sum of previous window sum. You need not to go to calculate whole sum again.

Example

1 2 3 4 5

First window = 1 2 3, sum=6

For next window, subtract 1 from sum, and add 4 to remaining sum.
Second window = 2 3 4
  i.e. 6 - 1 + 4 = 9

In this way, we are effectively moving our window from begining to end and we need to keep the max sum available till each window.

Lets look at the code.

Code

public int findMaxSum(int[] arr, int k) {
  int max = 0;
  int left = 0;
  int right = 0;

  int window_sum = 0;
  while (right < arr.length) {
    window_sum += arr[right];
    if (right >= k) {
      max = Math.max(max, window_sum);

      //subtract first number of previous widow
      window_sum -= arr[left];
      
      //move left pointer to next number
      left ++;
    }
  }

  return max;
}

We are keeping two pointers for window left and right. On completing the window size, we subtract first number of last window and keep a tab of the max sum available.

Complexity

We are iterating over array just once. Its O(n)