Heap Sort Algorithm
This is another very useful sorting algorithm based on Heap data structure. Read…
Young Tableau problem - Cormen
July 12, 2019
Young Tableau
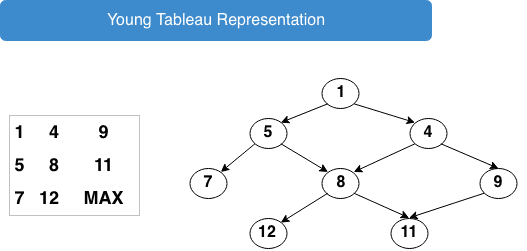
A a X b matrix is Young Tableau if all rows(from left to right) and columns(from top to bottom) are sorted. Some of the entries in matrix can be an INFINITY (MAX) value to represent that its not a valid value.
Example
1 5 9
4 7 11
8 12 MAX Operations supported on Young Tableau
There are majorly three operations supported here:
1. Prepare Young Tableau from a given 2-d array or a matrix
Given an input matrix, you want to make it honor young tableau property.
2. Extract a minimum value (and delete it)
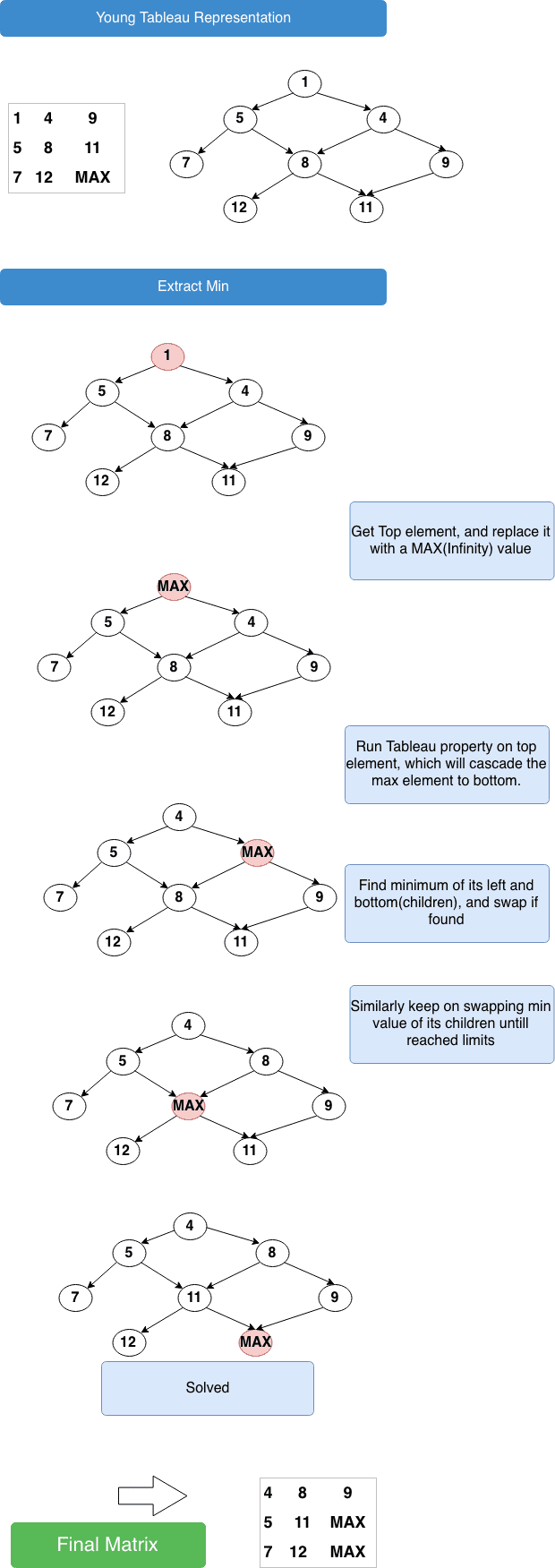
The minimum that resides on (0,0) position. Return it, and delete from matrix. We need to do some swap operations in order to make this matrix again as Young Tableau.
3. Search an element in young tableau
Given an element, we need to search in matrix and return its index in matrix.
Basic Building Pieces
Before we get started, lets understand some basics. This problem can be considered as a modified case of Min-Heap data structure. Where all elements below the root element are lesser. Here, we the the children of a matrix cell will be its right and bottom cells.
Some basic operations
/**
* Return [-1,-1], if there is no child element
*/
private int[] getLeft(int r, int c) {
if (r >= this.size-1) {
return new int[]{-1, -1};
}
return new int[]{r+1, c};
}
/**
* Return [-1,-1], if there is no child element
*/
private int[] getRight(int r, int c) {
if (c >= this.size-1) {
return new int[]{-1, -1};
}
return new int[]{r, c+1};
}
/**
* Check if the cell is within the matrix
*/
private boolean isCellValid(int[] cell) {
return cell[0]>=0 && cell[0]<this.size && cell[1]>=0 && cell[1]<this.size;
}Min Heapify operation
private void tableau_heapify(int r, int c) {
int[] left = this.getLeft(r, c);
int[] right = this.getRight(r, c);
int[] smallest = new int[]{r, c};
// System.out.println(r + ", " + c);
//check if the cell is less than both of its children
if (this.isCellValid(left) && this.matrix[left[0]][left[1]] < this.matrix[r][c]) {
//save address of left cell
smallest = left;
}
if (this.isCellValid(right) && this.matrix[right[0]][right[1]] < this.matrix[smallest[0]][smallest[1]]) {
//save address of right cell
smallest = right;
}
//Check if we found changed address in our smallest variables.
//If yes, swap them. And, recursively call this method on that cell address
if (this.isCellValid(smallest) && (smallest[0] != r || smallest[1] != c)) {
//swap
int t = this.matrix[r][c];
this.matrix[r][c] = this.matrix[smallest[0]][smallest[1]];
this.matrix[smallest[0]][smallest[1]] = t;
// recursive call tableau_heapify
this.tableau_heapify(smallest[0], smallest[1]);
}
}It runs on an cell index, and check whether both children cells are lesser than or not. If not, swap with the minimum cell value, and keep on moving like this in recursion. Key points for heapify operation:
- Get position of left and right children, and check if they are valid indexes (not crossing the matrix bounds)
- Check, if any children is having a lesser value.
- If found lesser value cell. Swap with it, and go in recursion.
- Note, if both children are smaller. We will go with minimum value cell.
Extract Min
/**
* Get element at (0,0), and make matrix tableau_heapify again
*/
public int extractMin() {
int min = this.matrix[0][0];
//put a max value here, just to denote that it has been taken out.
this.matrix[0][0] = Integer.MAX_VALUE;
//lets maintain tableau property
this.tableau_heapify(0, 0);
//all is set
return min;
}Key points:
- We know the min element is at (0,0) index
- Get it, and replace it with an INFINITY(MAX) value.
- Call our heapify() on this index.
- return the min value.
Search an element
/**
* a recursive method to search an element
* @return null if not found
*/
private int[] search(int element, int[] currentCell) {
if (!this.isCellValid(currentCell)) {
return null;
}
int currentElement = this.matrix[currentCell[0]][currentCell[1]];
if (element == currentElement) {
return currentCell;
}
if (element < currentElement) {
// move left
// decrement col by 1
currentCell[1]--;
return this.search(element, currentCell);
}
else { //(element > currentElement) {
//move down
//increment row by 0
currentCell[0] ++;
return this.search(element, currentCell);
}
}
/**
* Search the given element and return its index in matrix
*/
public int[] searchElement(int element) {
//we will start from top right corner to find the element
return this.search(element, new int[]{0, this.size-1});
}Key points:
- A simple brute force approach could be that keep on traversing from (0,0), and row wise. We can find our element somewhere in matrix. However, this will take O(mxn) runtime complexity.
- An optimize approach can be if we can search either from left-bottom, or top-right, or bottom-right corner.
- In this algorithm, we start from top-right.
-
There can be three cases:
- Either number found, just return it
- Number in current cell is greater. Simply goto its left. As, complete column is sorted. We cannot find it in this column.
- Number in current cell is lesser. Simply goto its bottom. As, complete row is sorted. Every element in left hand side will be lesser.
- Do this in recursion, and either we find it, or not find it.
Image representation
Complete Code
public class YoungTableau {
private int[][] matrix;
private int size;
public YoungTableau(int[][] matrix, int size) {
this.matrix = matrix;
this.size = size;
//build young tableau from given matrix
this.buildYoungTableau();
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer();
for (int i=0; i<this.size; i++) {
for (int j=0; j<size; j++) {
sb.append(this.matrix[i][j]).append(" ");
}
sb.append("\n");
}
return sb.toString();
}
/**
* Return [-1,-1], if there is no child element
*/
private int[] getLeft(int r, int c) {
if (r >= this.size-1) {
return new int[]{-1, -1};
}
return new int[]{r+1, c};
}
/**
* Return [-1,-1], if there is no child element
*/
private int[] getRight(int r, int c) {
if (c >= this.size-1) {
return new int[]{-1, -1};
}
return new int[]{r, c+1};
}
/**
* Check if the cell is within the matrix
*/
private boolean isCellValid(int[] cell) {
return cell[0]>=0 && cell[0]<this.size && cell[1]>=0 && cell[1]<this.size;
}
/**
* Main the property of young tableau
*/
private void tableau_heapify(int r, int c) {
int[] left = this.getLeft(r, c);
int[] right = this.getRight(r, c);
int[] smallest = new int[]{r, c};
// System.out.println(r + ", " + c);
//check if the cell is less than both of its children
if (this.isCellValid(left) && this.matrix[left[0]][left[1]] < this.matrix[r][c]) {
//save address of left cell
smallest = left;
}
if (this.isCellValid(right) && this.matrix[right[0]][right[1]] < this.matrix[smallest[0]][smallest[1]]) {
//save address of right cell
smallest = right;
}
//Check if we found changed address in our smallest variables.
//If yes, swap them. And, recursively call this method on that cell address
if (this.isCellValid(smallest) && (smallest[0] != r || smallest[1] != c)) {
//swap
int t = this.matrix[r][c];
this.matrix[r][c] = this.matrix[smallest[0]][smallest[1]];
this.matrix[smallest[0]][smallest[1]] = t;
// recursive call tableau_heapify
this.tableau_heapify(smallest[0], smallest[1]);
}
}
private void buildYoungTableau() {
for (int i=this.size-1; i>=0; i--) {
for (int j=this.size-1; j>=0; j--) {
this.tableau_heapify(i, j);
}
}
}
/**
* Get element at (0,0), and make matrix tableau_heapify again
*/
public int extractMin() {
int min = this.matrix[0][0];
//put a max value here, just to denote that it has been taken out.
this.matrix[0][0] = Integer.MAX_VALUE;
//lets maintain tableau property
this.tableau_heapify(0, 0);
//all is set
return min;
}
/**
* a recursive method to search an element
* @return null if not found
*/
private int[] search(int element, int[] currentCell) {
if (!this.isCellValid(currentCell)) {
return null;
}
int currentElement = this.matrix[currentCell[0]][currentCell[1]];
if (element == currentElement) {
return currentCell;
}
if (element < currentElement) {
// move left
// decrement col by 1
currentCell[1]--;
return this.search(element, currentCell);
}
else { //(element > currentElement) {
//move down
//increment row by 0
currentCell[0] ++;
return this.search(element, currentCell);
}
}
/**
* Search the given element and return its index in matrix
*/
public int[] searchElement(int element) {
//we will start from top right corner to find the element
return this.search(element, new int[]{0, this.size-1});
}
public static void main(String[] args) {
int[][] matrix = {
{12, 7, 11},
{8, 9, 1},
{4, 5, Integer.MAX_VALUE}
};
YoungTableau t = new YoungTableau(matrix, 3);
System.out.println(t);
System.out.println("------------------");
System.out.println("Searching index of 8: " + ArrayUtils.toString(t.searchElement(8)));
System.out.println("Searching index of 12: " + ArrayUtils.toString(t.searchElement(12)));
System.out.println("Searching index of 4: " + ArrayUtils.toString(t.searchElement(4)));
System.out.println("Searching index of 1: " + ArrayUtils.toString(t.searchElement(1)));
System.out.println("Min: " + t.extractMin());
System.out.println("------------------");
System.out.println(t);
System.out.println("------------------");
System.out.println("Min: " + t.extractMin());
System.out.println("------------------");
System.out.println(t);
System.out.println("------------------");
System.out.println("Min: " + t.extractMin());
System.out.println("------------------");
System.out.println(t);
System.out.println("------------------");
System.out.println("Min: " + t.extractMin());
System.out.println("------------------");
System.out.println(t);
System.out.println("------------------");
}
}Similar Posts
Longest Palindrome Substring - Leet Code Solution
Problem Statement Given a string s, find the longest palindromic substring in s…
Reverse digits of a signed integer - Leet Code Solution
Problem Statement Given a signed integer, reverse digits of an integer. Return…
Add two numbers(reverse order) link list Problem - Leet Code Solution
Problem Statement You are given two non-empty linked lists representing two non…
Longest Common Prefix - Leet Code Solution
Problem Statement Write a function to find the longest common prefix string…
Selection Sort Algorithm
It is one of a simple algorithm to study for a beginner to understanding sorting…
Latest Posts
Leetcode - Rearrange Spaces Between Words
Problem Statement You are given a string text of words that are placed among…
Leetcode - Maximum Non Negative Product in a Matrix
Problem Statement You are given a rows x cols matrix grid. Initially, you are…
Leetcode - Split a String Into the Max Number of Unique Substrings
Problem Statement Given a string s, return the maximum number of unique…
Crawler Log Folder - minimum number of operations needed to go back to the main folder after the change folder operations.
Problem The Leetcode file system keeps a log each time some user performs a…
Replace all spaces in a string with %20
Problem Statement Replace all spaces in a string with ‘%20’ (three characters…
Determine if a string has all unique characters
Problem Implement an algorithm to determine if a string has all the characters…