Merge Sort Algorithm

This algorithm is very efficient one, and is classic example of Divide and Conquer algorithms.

In this algorithn, we divide the whole array into smaller sub-problems. i.e. till we get only single element. Single element means, there is no need to sort it. Lets call it sorted sub-array.

Next step is to merge two such sorted sub-array. The operation is called merge two sorted arrays.

As, the recursion stacks pops-up. We keeps on merging sorted sub-arrays. Untill all sub-arrays merged into one.

Finally we get the sorted array.

Merge Sort Algorithm

• First method takes array and index of array as first and last index.
• Divide the array into two equal half.
• Recursive call to same function with the left half array.
• Recursive call to same function with the right half array.
• Now, we get sorted sub-array. Note: each single element is itself sorted.
• Next step is to merge two sorted sub-arrays.
• We keep on doing this, untill all sub-arrays merged to become one.

See the code here:

public void doMergeSort(int[] arr, int l, int r) {
    if (l < r) {
        int m = (r+l)/2;
        
        doMergeSort(arr, l, m);
        doMergeSort(arr, m+1, r);
        
        merge(arr, l, m, r);
    }
}

private void merge(int[] a, int l, int m, int r) {
    int[] left = new int[m-l+1];
    int[] right = new int[r-m];
    
    for (int i=l; i<=m; i++) {
        left[i-l] = a[i];
    }
    for (int i=m+1; i<=r; i++) {
        right[i-m-1] = a[i];
    }
    
    int lindex = 0;
    int rindex = 0;
    for (int i=l; i<=r; i++) {
        if (lindex < left.length && (rindex >= right.length || left[lindex] < right[rindex])) {
            a[i] = left[lindex];
            lindex ++;
        }
        else {
            a[i] = right[rindex];
            rindex ++;
        }
    }
}

In above merge method, I have handled all cases in same loop. There is an alternate solution to this as well, see below:

public void merge2(int[] a, int l, int m, int r) {
    int l1 = m-l+1;
    int l2 = r-m;
    int[] left = new int[l1];
    int[] right = new int[l2];
    
    for (int i=0; i<l1; i++) {
        left[i] = a[l+i];
    }
    for (int i=0; i<l2; i++) {
        right[i] = a[m+1+i];
    }
    
    int lindex = 0;
    int rindex = 0;
    int i=l;
    while (lindex < l1 && rindex < l2) {
        if (left[lindex] < right[rindex]) {
            a[i] = left[lindex];
            lindex++;
        }
        else {
            a[i] = right[rindex];
            rindex++;
        }
        i++;
    }
    
    //copy the leftover array
    for (int j=lindex; j<l1; j++) {
        a[i] = left[j];
        i++;
    }
    for (int j=rindex; j<l2; j++) {
        a[i] = right[j];
        j++;
    }
}

Graphical Example

Key Points

• Its a great algorithm to sort Link lists, because this algorithm does not rely on accessing values by indexes.
• It takes extra memory in merge method.
• Very efficient in sorting large number set
• Performance is very good. its complexity is O(n log n)
• Based on Divice and Conquer technique
• Its a stable sort algorithm

Runtime complexity

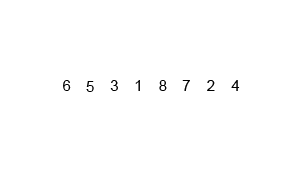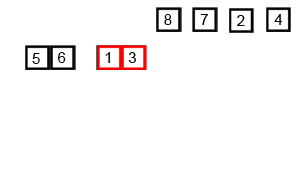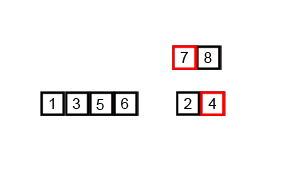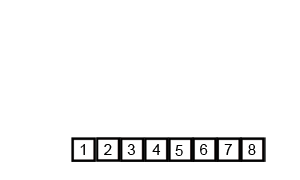
The algorithm runs on O(n log n) in worst/average case.

The merge function runs in O(n) time. Lets look at doMergeSort method which divides the input array. It divides the array into equal halves each time. First n/2, then (n/2)/2=n/4, then n/8, then n/16 and so on.

Which evaluates to log n So, total complexity of O(n log n)